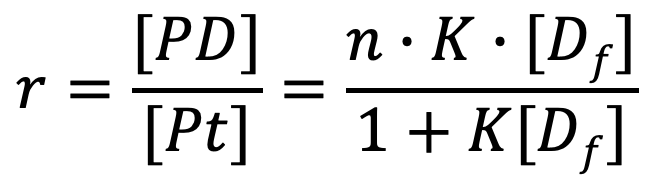
Contents
血漿タンパク結合率は一定じゃない!結合部位が埋まっると非結合形が溢れる。
血漿タンパクと結合していると組織中に薬は入れないので、薬理作用には、非結合形の濃度が重要です。
しかし、タンパク質の結合部位数には限りがあります。
薬の濃度が高くなると一気に非結合形が増え、副作用域に突入してしまう可能性があります。
今回は、結合数と非結合形薬の濃度の関係について学びます。
薬の非結合形と結合形の割合については、こちらをご覧ください
-
-
分布容積とタンパク結合率をゴロとイメージでわかりやすく解説
📘 関連教材 薬剤マインドマップPDF 説明欄にサンプルPDFもあります。薬剤科目をマインドマップにまとめました。 🛒 今すぐ見る Contents分布容積とは、理論上の体液量のこと分布容積を全体液量 ...
続きを見る
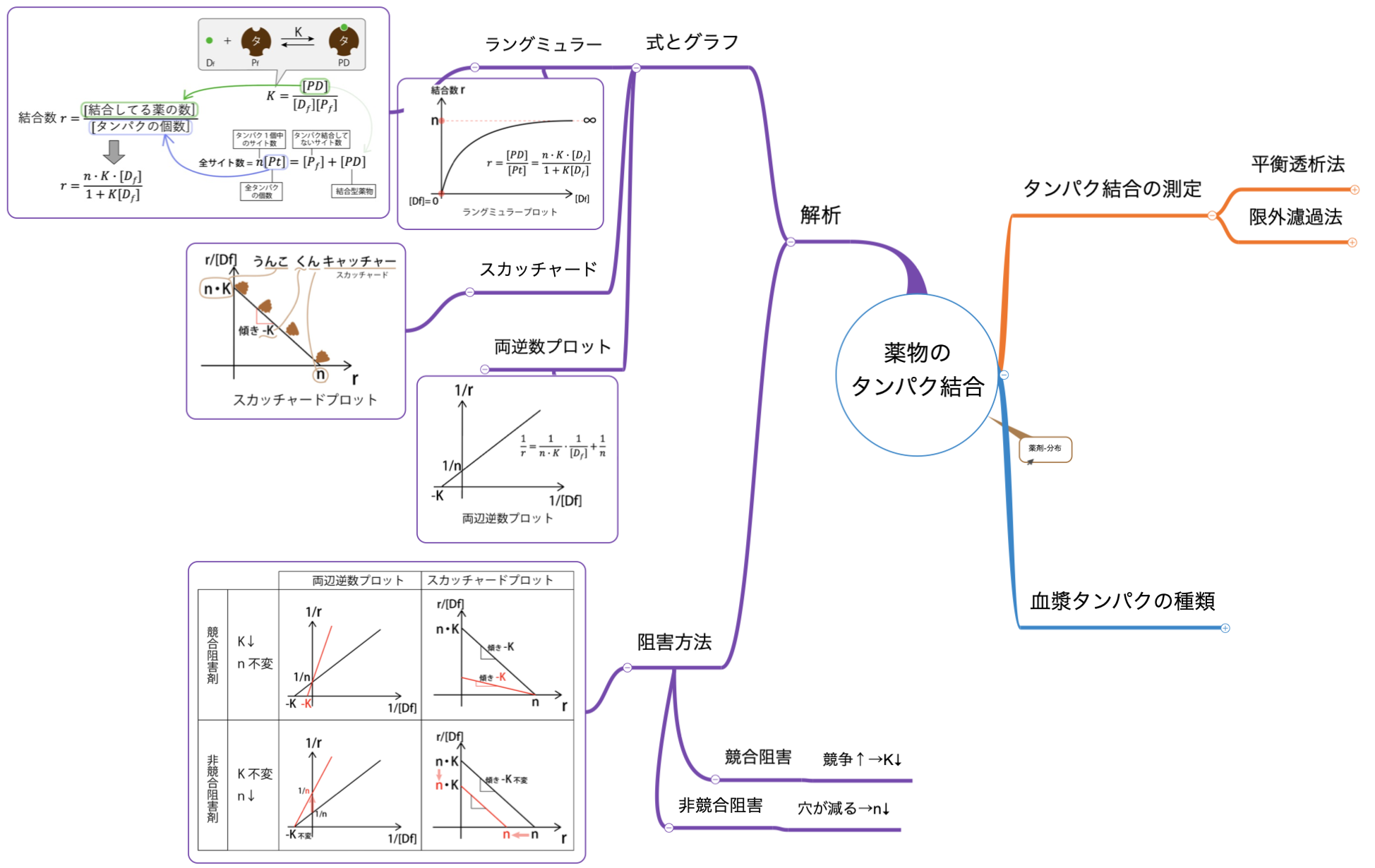
到達目標は式からグラフが書けるようになること
まずは、今回のゴールを提示しておきます。
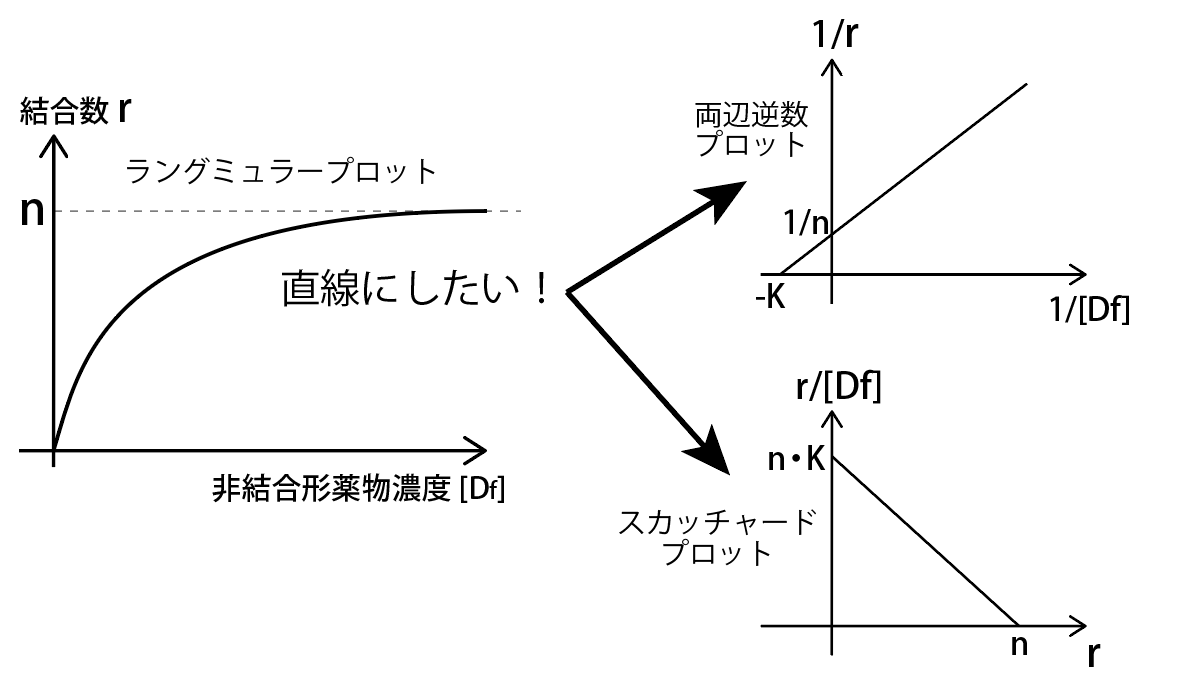
結合数rと非結合薬物濃度[Df]には何らかの関係があります。


ラングミュラー式を見やすく直線に式変形したのがスカッチャードプロットと両辺逆数プロットです。
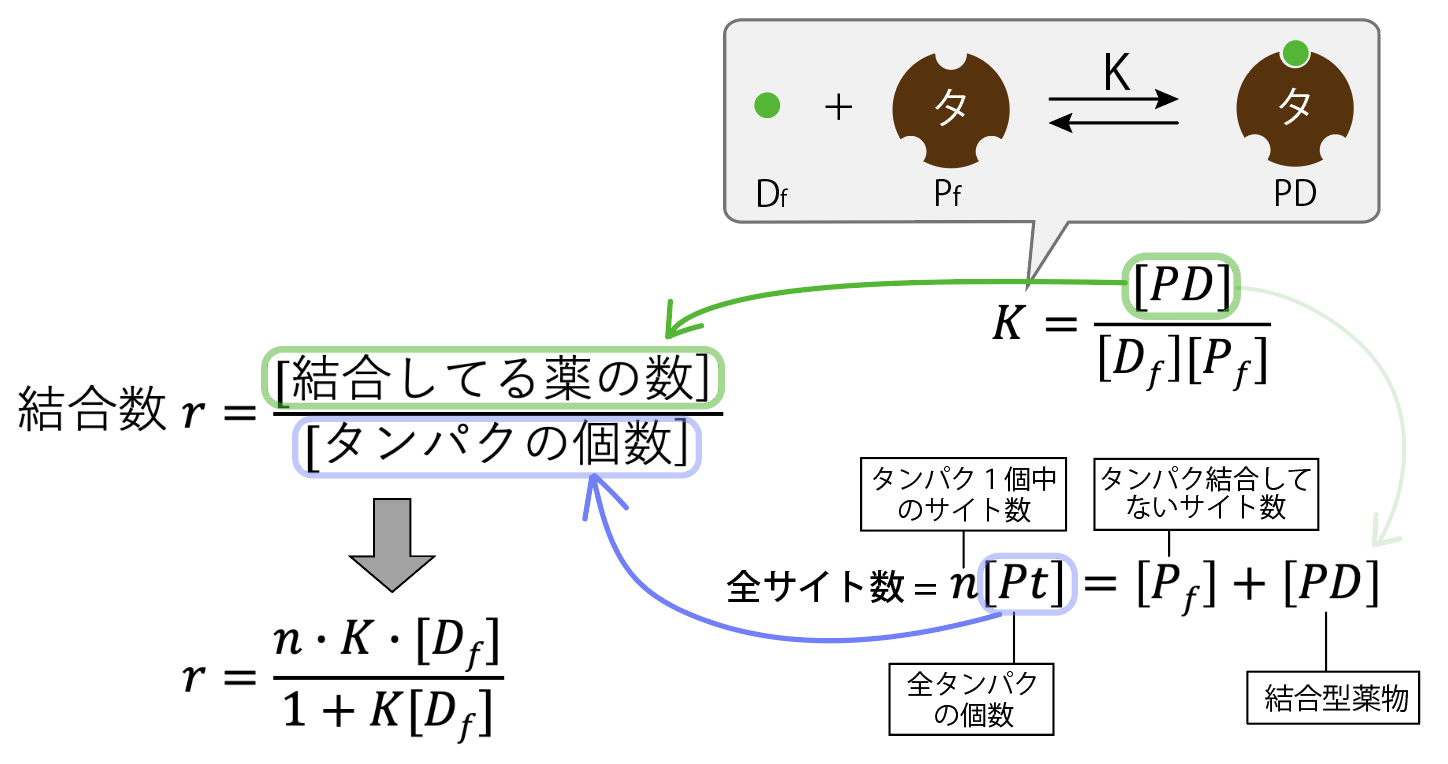
結合数r=結合してる薬の数÷タンパクの個数
ラングミュア式を求めるのは意外と簡単です。

あとは、平衡定数の関係式と、タンパクの個数の関係式を代入したら出ます。細かい導出は後半で。
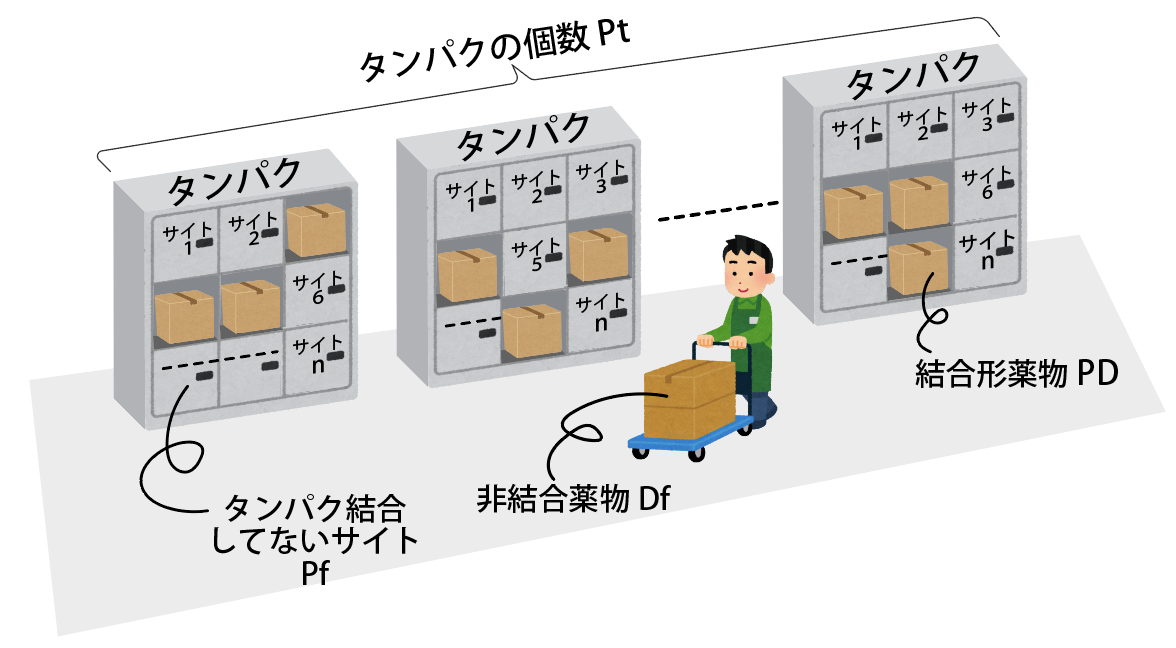
補足:用語のイメージ
マンションの宅配ボックスのイメージです。
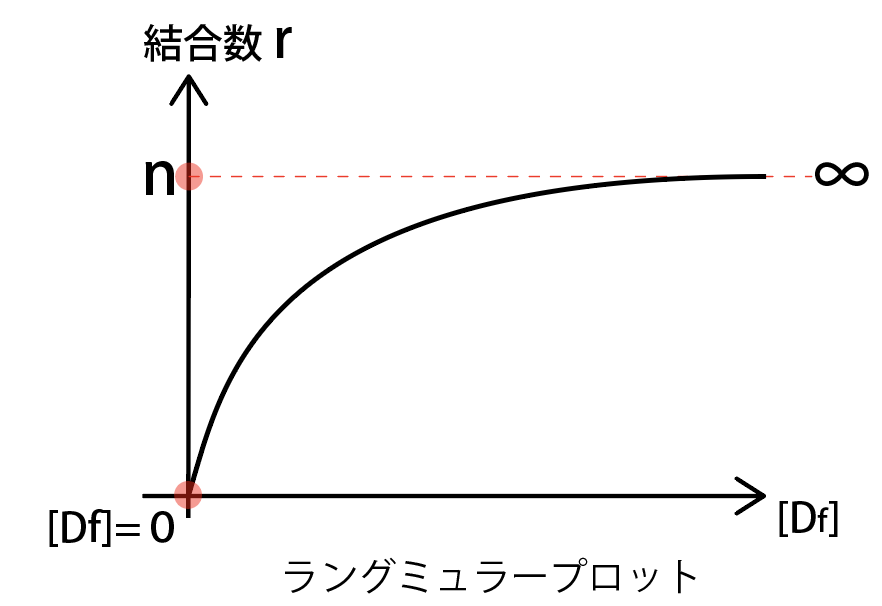
Langmuir(ラングミュア)式からグラフへ
ラングミュア式を見てみましょう。
- [Df]=0の時、r=0
- [Df]→∞の時、
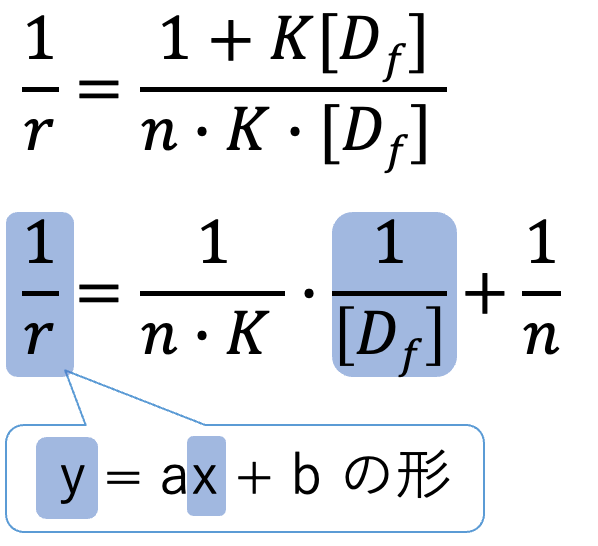
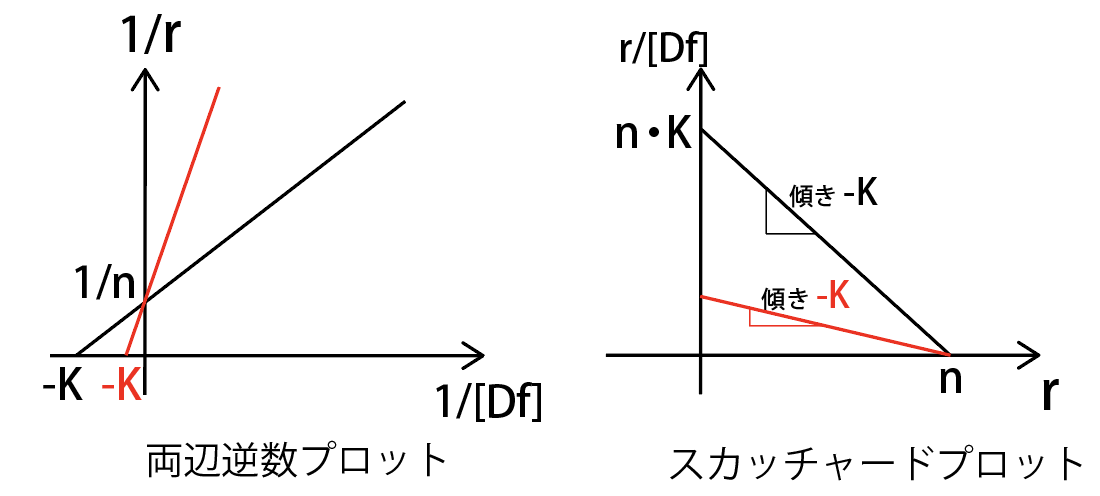
Langmuir(ラングミュア)式を直線に直す
両辺逆数プロットはひっくり返しただけ
ラングミュア式の分母の足し算が鬱陶しいので、分子分母をひっくり返します。
- y軸切片=1/n→タンパクの結合部位数n がわかりる
- x軸切片=-K →結合定数K がわかる
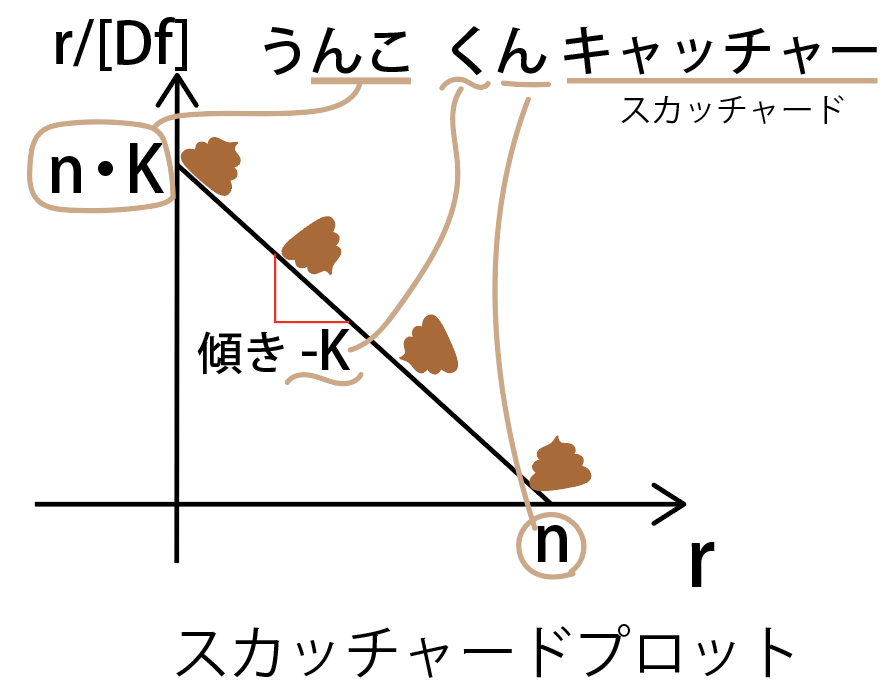
Scatchard(スカッチャード)プロットは語呂「うんこ君キャッチャー」で覚える

スカッチャードプロットのゴロは、「うんこくんキャッチャー」です。
左上からうんこ君が転がり落ちるイメージです。
- y切片:n・K
- 傾き:-K
- x切片:n
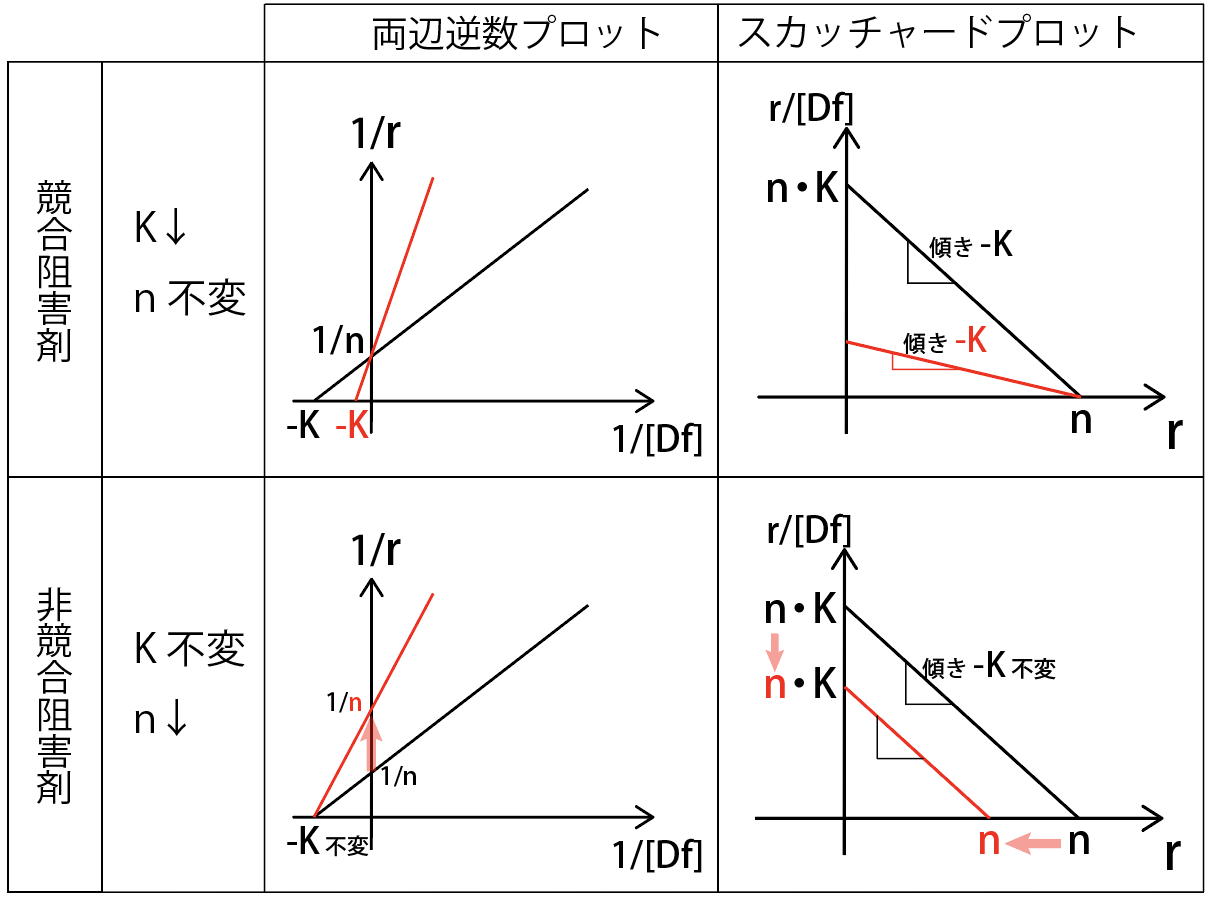
競合阻害と非競合阻害
阻害剤を入れたときのグラフの変化が問われます。
まず、阻害剤を入れると血漿タンパクに何が起きるかみてみましょう。
競合阻害剤
競合阻害剤は、単純な穴の奪い合いです。
- 穴を奪い合い、結合形が減るので、平衡定数Kが下がります。
- タンパクの結合部位数 n は不変です。

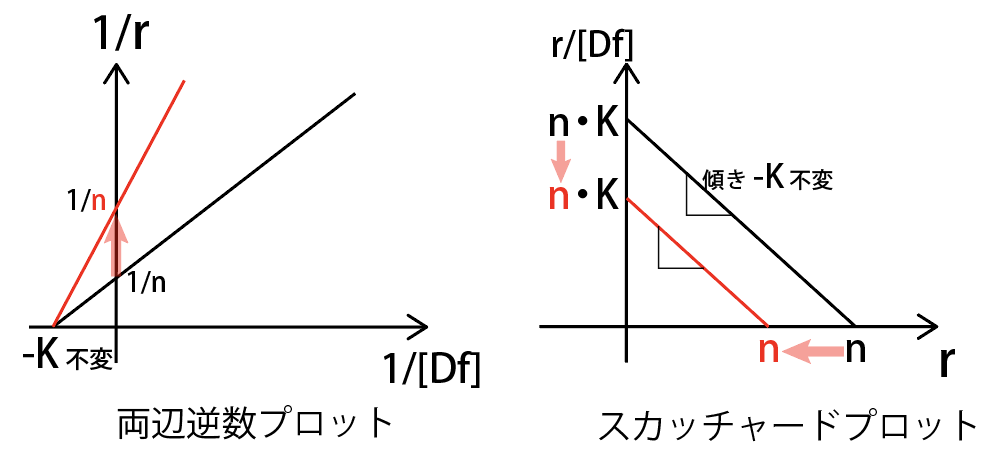
非競合阻害剤
非競合阻害剤を入れると、
- タンパク質に変化が生じ、結合数 r が下がります。
- 結合定数 K は不変
グラフは
グラフの変化のまとめ
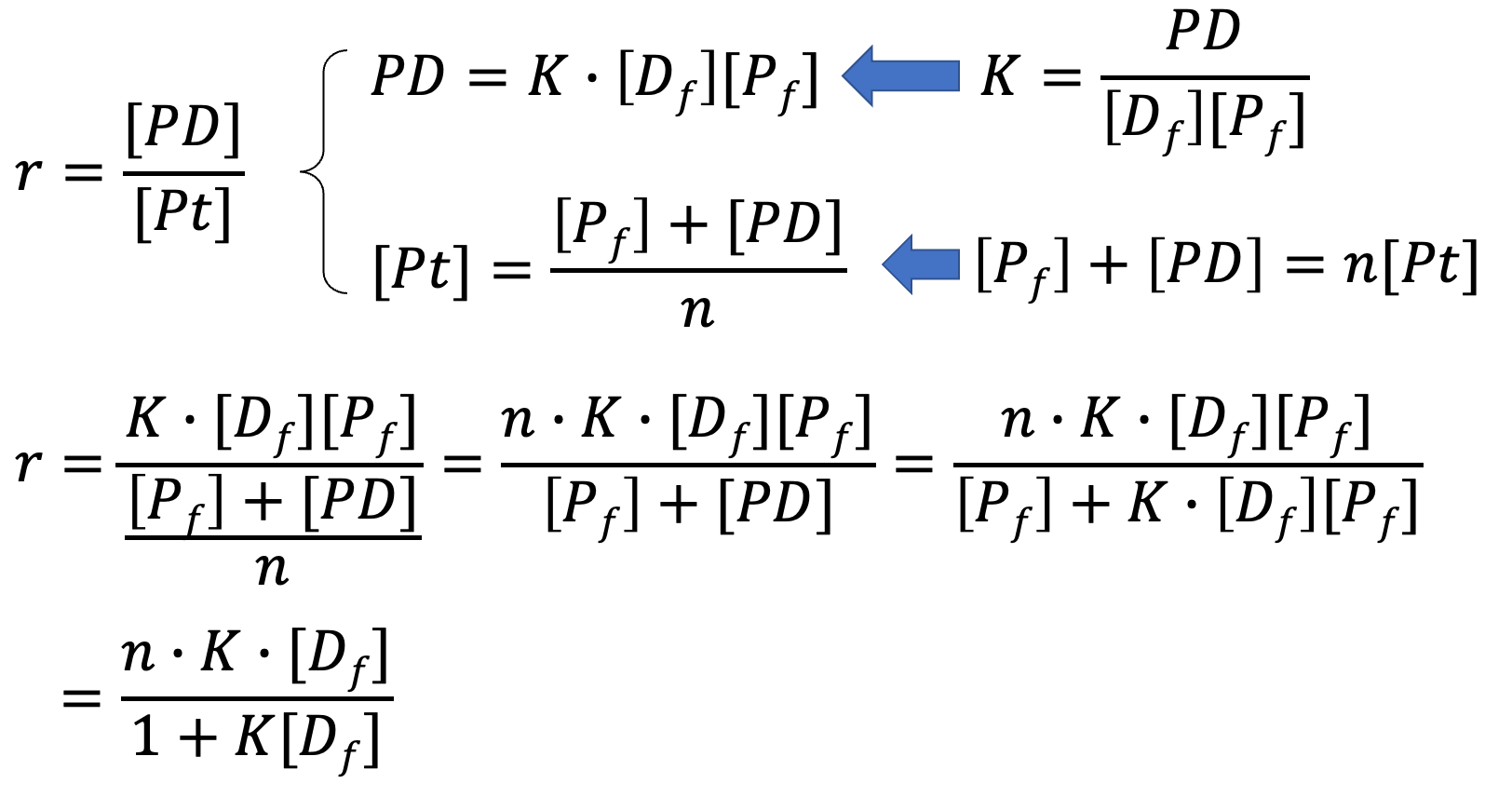
参考:ラングミュラーの式の導出
ラングミュラーの式の導出を載せておきます。
自分の手で導出しておくと忘れにくいです。
グラフが頭に入っていて、
- 結合形薬[Df]と結合数rの関係式で
- nに収束する
- 初めは0
になるような式と覚えていれば、グラフからもラングミュラー式を思い出しやすくなります。
まとめ
ラングミュラーの式は、結合数rと結合形薬[Df]の関係を平衡定数・結合部位数の関係式を併せて表現したものでした。
ラングミュラー式からグラフにし、
ラングミュラー式を変形して、グラフが直線になる両辺逆数プロット、スカッチャードプロットが導かれました。
競合阻害剤・非競合阻害剤を併用したときに起こるタンパクの変化を理解すれば、グラフの変化も覚えずとも描けます。